Counters: Asynchronous and Synchronous

Introduction

Imagine you're at a turnstile counting people entering a stadium, or a digital clock ticking away seconds, or a CPU keeping track of instruction cycles. All these scenarios need counters—sequential circuits that go through a defined sequence of states with each clock pulse.

Counters are everywhere in digital systems:

• Timers and clocks
• Frequency dividers
• Address generators for memory
• Event counters
• Digital frequency meters
• Sequence generators

Why Counters Matter

Counters are among the most widely used sequential circuits. Understanding them gives you the foundation for building more complex systems like state machines, timers, and control units. Every digital clock you've ever seen is built around counters!

Counter Fundamentals

What is a Counter?

A counter is a sequential circuit that progresses through a predetermined sequence of states upon receiving input clock pulses.

Basic Properties:

• Built from flip-flops (usually T or JK)
• Has a defined sequence (usually binary)
• Advances on clock edges
• Can count up or down
• May have additional control inputs (reset, load, enable)

Counter Classification:

Counters
├── By Direction
│   ├── Up Counters (0→1→2→3...)
│   ├── Down Counters (3→2→1→0...)
│   └── Up-Down Counters (bidirectional)
├── By Clocking
│   ├── Asynchronous (Ripple)
│   └── Synchronous
└── By Sequence
    ├── Binary (follows binary sequence)
    └── Non-Binary (arbitrary sequence)

Modulus of a Counter

The modulus (MOD) is the number of states in the counter's sequence.

Counter Type	Modulus	States	Bits Required
MOD-2	2	0, 1	1
MOD-4	4	0, 1, 2, 3	2
MOD-8	8	0-7	3
MOD-10	10	0-9	4
MOD-16	16	0-15	4
MOD-N	N	0 to N-1	⌈log₂N⌉

Relationship:

$$\text{Number of flip-flops} = \lceil \log_2(\text{Modulus}) \rceil$$

Example: MOD-10 counter needs ⌈log₂10⌉ = ⌈3.32⌉ = 4 flip-flops

Asynchronous Counters (Ripple Counters)

3-Bit Asynchronous Binary Counter

The simplest counter: uses two T flip-flops.

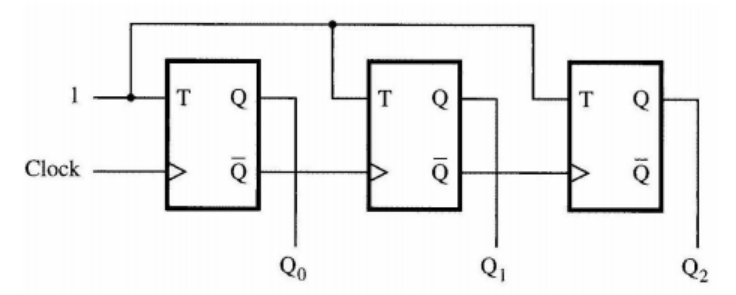
Operation:

• FF0 toggles on every external clock rising edge
• FF1 toggles on every FF0 falling edge (Q0: 1→0 transition)
• Creates divide-by-2 then divide-by-2 again = divide-by-4 overall

State Sequence:

CLK Pulse	Q2 Q1 Q0	Decimal
0	0 0 0	0
1	0 0 1	1
2	0 1 0	2
3	0 1 1	3
4	1 0 0	4
5	1 0 1	5
6	1 1 0	6
7	1 1 1	7
8	0 0 0	0 (wraps around)

Why "Ripple"?

Called "ripple" counter because the clock "ripples" through the flip-flops like a wave—each FF clocks the next one. This creates propagation delay accumulation.

4-Bit Asynchronous Binary Counter (MOD-16)

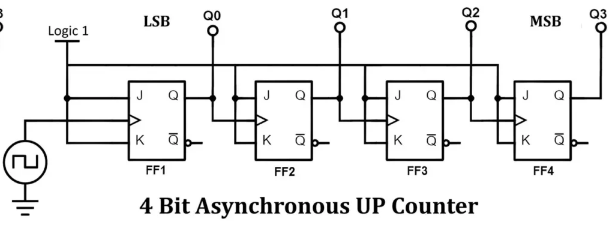
Characteristics:

• Modulus: 16 (counts 0-15)
• States: 0000 to 1111 in binary
• Frequency division: Output frequency = Input frequency / 16
• Q0 changes at CLK rate (LSB)
• Q3 changes at CLK/8 rate (MSB)

State Sequence (partial):

CLK	Q3	Q2	Q1	Q0	Decimal
0	0	0	0	0	0
1	0	0	0	1	1
2	0	0	1	0	2
3	0	0	1	1	3
4	0	1	0	0	4
...	...	...	...	...	...
15	1	1	1	1	15
16	0	0	0	0	0

Propagation Delay in Ripple Counters

Major Limitation: Accumulated delay through cascaded flip-flops.

Total Propagation Delay:

$$t_{total} = n \times t_{pd(FF)}$$

Where:

• n = number of flip-flops
• t_pd(FF) = propagation delay of one flip-flop

Example:

• 4-bit counter
• Each FF has t_pd = 10ns
• Total delay = 4 × 10ns = 40ns

Problem: At high frequencies, next clock pulse may arrive before all FFs have settled—causing errors!

Maximum Frequency:

$$f_{max} = \frac{1}{n \times t_{pd(FF)}}$$

For 4-bit counter with 10ns FF delay:

$$f_{max} = \frac{1}{40ns} = 25\,MHz$$

Speed Limitation

Asynchronous counters are slow because of cumulative delay. For high-speed applications (>50MHz), use synchronous counters instead!

MOD-N Asynchronous Counter

To create a counter with modulus other than 2^n, add reset logic.

MOD-10 Counter (Decade Counter) Example:

Goal: Count 0-9, then reset to 0

Approach:

1. Start with 4-bit counter (can count 0-15)
2. Detect when count reaches 10 (1010 in binary)
3. Asynchronously clear all flip-flops

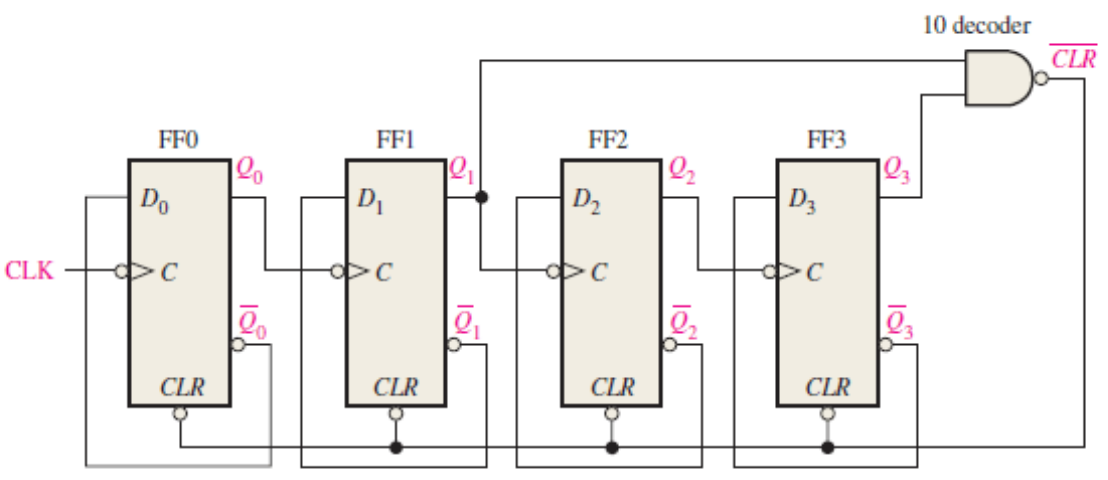
Detection Logic:

• Decimal 10 = 1010 binary = Q3=1, Q2=0, Q1=1, Q0=0
• Use NAND gate: Q3 · Q1 = 1 only when count = 10, 11, 14, or 15
• Counter resets before reaching 11, so only 10 triggers reset

State Sequence:

CLK	Q3 Q2 Q1 Q0	Decimal	Notes
0-9	0000-1001	0-9	Normal counting
10	1010	10	Briefly appears then resets
10+	0000	0	Reset to 0

Reset Glitch

The counter briefly enters state 10 before resetting. This ~10ns glitch can cause problems in some applications. Solution: Use synchronous counter or add output register.

Asynchronous Down Counter

To count down instead of up, clock each FF from the Q̄ output of the previous FF.

Circuit Modification:

FF0 Q̄ → FF1 CLK
FF1 Q̄ → FF2 CLK
etc.

State Sequence: 15→14→13→...→1→0→15...

Synchronous Counters

Key Difference

In synchronous counters, all flip-flops are clocked simultaneously by the same clock signal. This eliminates propagation delay accumulation!

Advantages:

• ✅ Much faster (no accumulated delays)
• ✅ No glitches between states
• ✅ Easier timing analysis
• ✅ Better for high-speed designs

Disadvantage:

• ❌ More complex logic required (but worth it!)

2-Bit Synchronous Binary Counter

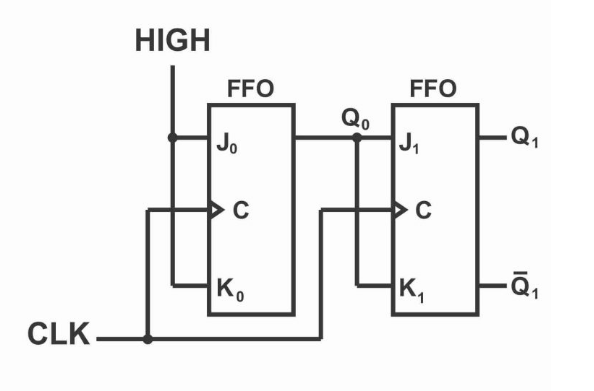
Operation Logic:

• LSB (Q0) toggles every clock cycle
• MSB (Q1) toggles only when Q0=1

Truth Table for Next State:

Current (Q1 Q0)	Next (Q1 Q0)	J0 K0	J1 K1
0 0	0 1	1 1	0 0
0 1	1 0	1 1	1 1
1 0	1 1	1 1	0 0
1 1	0 0	1 1	1 1

4-Bit Synchronous Binary Counter

Design Rules for Binary Up Counter:

• Each FF toggles when all lower FFs are 1
• FF_n toggles when Q_(n-1) · Q_(n-2) · ... · Q_0 = 1

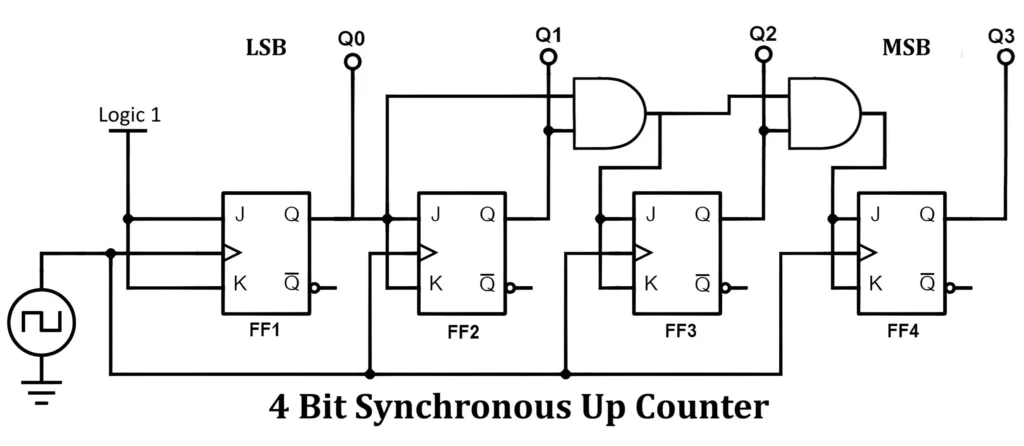
Propagation Delay:

• Only one flip-flop delay regardless of counter size!
• Maximum frequency much higher than ripple counter

Example Timing:

• Ripple counter: 40ns total delay (10ns × 4 FFs)
• Synchronous counter: 10ns total delay (one FF only)
• Synchronous is 4× faster for 4-bit counter!

Synchronous is Standard

In modern digital design (FPGAs, microcontrollers), synchronous counters are the norm. Asynchronous counters are mainly for learning or very specific low-speed applications.

Synchronous MOD-N Counters

To create MOD-N synchronous counter:

1. Use sufficient flip-flops: ⌈log₂N⌉
2. Add logic to reset or skip states after (N-1)

MOD-10 Synchronous Counter:

Approach 1: Synchronous Clear

• Detect count = 9
• On next clock, load 0 into all FFs

Approach 2: Synchronous Load

• Use counter with parallel load
• When count = 9, load 0 on next clock

Up-Down Counter

Up-Down counter can count in either direction based on control signal.

Design Approach:

• Add multiplexers to select increment or decrement logic
• UP signal selects which logic path is active

Applications:

• Position tracking (encoder systems)
• Reversible timers
• Bidirectional event counting

Commercial ICs:

• 74HC191: Synchronous up/down counter
• 74HC193: Synchronous 4-bit binary up/down counter

Presettable Counters

Presettable counters can be loaded with an initial value.

Inputs:

• LOAD: Control signal to load data
• D3 D2 D1 D0: Parallel data inputs
• CLK: Clock signal

Operation:

• When LOAD=1: On next clock, load D inputs into counter
• When LOAD=0: Normal counting

Applications:

• Starting count from specific value
• Implementing countdown timers
• Creating custom sequences

Counter Applications

1. Frequency Divider

Most Common Application: Divide input frequency by power of 2.

Circuit:

• N-bit counter
• Output Q_(N-1) has frequency = f_input / 2^N

Example:

• 4-bit counter
• Input: 16 MHz
• Q0 output: 8 MHz (÷2)
• Q1 output: 4 MHz (÷4)
• Q2 output: 2 MHz (÷8)
• Q3 output: 1 MHz (÷16)

2. Digital Clock

Design: Cascade multiple counters

1 Hz input → MOD-60 counter (seconds) →
             MOD-60 counter (minutes) →
             MOD-24 counter (hours)

3. Event Counter

Count external events (button presses, sensor triggers, etc.)

Circuit:

• Counter
• Input: Event signal
• Output: Number of events counted
• Display: 7-segment or LCD

4. Sequence Generator

Generate specific sequences for control logic.

Example: Traffic Light Controller

State 0: Green (30 sec)
State 1: Yellow (5 sec)
State 2: Red (30 sec)

Use counter + decoder to generate states.

5. PWM Generation

Use counter + comparator to generate PWM signals.

Ring Counters and Johnson Counters

Ring Counter

Ring counter: Shift register with output fed back to input.

4-Bit Ring Counter States:

CLK	Q3	Q2	Q1	Q0
0	0	0	0	1
1	0	0	1	0
2	0	1	0	0
3	1	0	0	0
4	0	0	0	1

Characteristics:

• Modulus: N (same as number of flip-flops)
• Advantage: One-hot outputs (only one HIGH at a time)
• Disadvantage: Inefficient (needs N FFs for MOD-N)

Applications:

• State machines where one-hot encoding simplifies logic
• Stepper motor control
• Sequential control circuits

Johnson Counter (Twisted Ring Counter)

Johnson counter: Ring counter with inverted feedback.

4-Bit Johnson Counter States:

CLK	Q3	Q2	Q1	Q0	Decimal
0	0	0	0	0	0
1	0	0	0	1	1
2	0	0	1	1	3
3	0	1	1	1	7
4	1	1	1	1	15
5	1	1	1	0	14
6	1	1	0	0	12
7	1	0	0	0	8
8	0	0	0	0	0

Characteristics:

• Modulus: 2N (twice the number of flip-flops!)
• More efficient than ring counter
• Self-starting (can recover from invalid states)

Applications:

• Frequency dividers
• Sequence generators
• Switch debouncing

Counter ICs (Integrated Circuits)

Popular Counter ICs

IC Number	Type	Description
74HC161	Sync	4-bit binary, synchronous, presettable
74HC163	Sync	4-bit binary, synchronous, no async clear
74HC190	Sync	BCD up/down counter
74HC191	Sync	Binary up/down counter
74HC193	Sync	4-bit binary up/down counter
74HC390	Async	Dual decade counter
74HC393	Async	Dual 4-bit binary counter
CD4017	Decade	Johnson counter with 10 decoded outputs

74HC161 Synchronous Counter

Pinout and Features:

• 4-bit binary counter (0-15)
• Synchronous parallel load
• Synchronous clear
• Ripple carry output (for cascading)
• Clock enable input

Applications:

• Frequency division
• Address generation
• Timing and sequencing

Troubleshooting Counters

Common Problems

1. Counter Stuck at One State

• Check clock signal
• Verify power supply
• Test clear/reset inputs
• Check for damaged IC

2. Counter Skipping States

• Clock signal noise or bouncing
• Timing violations (setup/hold)
• Loose connections
• Decoupling capacitor missing

3. Irregular Counting

• Noisy power supply
• Improper grounding
• Clock frequency too high
• Damaged flip-flop

Debugging Techniques

Tools:

• Logic analyzer (best for viewing all signals simultaneously)
• Oscilloscope (for timing analysis)
• LED indicators (for slow counters)
• Multimeter (DC voltage checks)

Procedure:

1. Verify power supply (5V for TTL/CMOS)
2. Check clock signal (clean edges, correct frequency)
3. Test reset/clear functionality
4. Verify output states in sequence
5. Check for noise or glitches

Summary

Counters are essential sequential circuits that count clock pulses or events:

✅ Asynchronous (Ripple): Simple but slow due to accumulated delay
✅ Synchronous: Fast, no accumulated delay, industry standard
✅ MOD-N: Can count in any modulus with additional logic
✅ Up-Down: Can count in both directions
✅ Special: Ring and Johnson counters for specific applications

Key Takeaways:

1. Asynchronous: Easy to build, but speed-limited by ripple delay
2. Synchronous: Preferred for modern designs, much faster
3. Modulus: Determines the counting sequence length
4. Applications: Frequency division, timing, sequencing, counting
5. ICs: Ready-made counter ICs save design time

Next Steps

With counters mastered, we're ready to tackle shift registers—circuits that move data serially or in parallel. Shift registers are crucial for data conversion, storage, and communication!

Further Reading

• "Digital Design" by Morris Mano (Chapter on Counters)
• Datasheet study: 74HC161, 74HC193
• FPGA counter implementations in Verilog/VHDL
• Advanced topics: Gray code counters, Linear Feedback Shift Registers (LFSR)

---

Practice Problems:

1. Design a MOD-12 asynchronous counter
2. Calculate max frequency for 8-bit ripple counter (tpd = 8ns per FF)
3. Design a synchronous MOD-6 counter using JK flip-flops
4. How many flip-flops needed for MOD-100 counter?
5. Design a frequency divider: 10 MHz → 1 MHz
6. Draw timing diagram for 3-bit Johnson counter
7. Interface 74HC161 to create MOD-100 counter (cascade two ICs)